ローレンツ曲線とジニ係数

はじめに

今回は所得格差を表す指標であるローレンツ曲線とジニ係数について考えていきます。

これらは、所得格差を評価する際に有力な指標であり経済学を学ぶ上でとても重要です。

最初は難しいと感じるかもしれませんが定義をしっかりと理解して計算もできるように頑張りましょう。

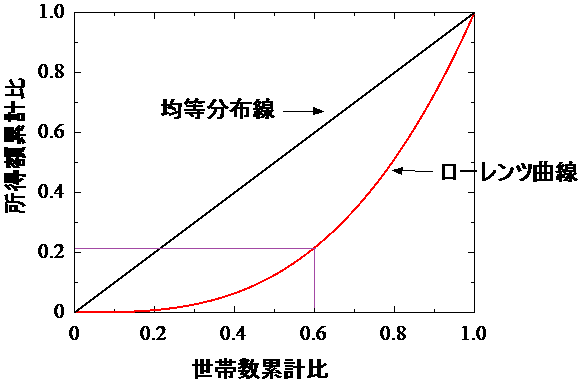
　ローレンツ曲線は、世帯を所得の低い順番に並べ、横軸に世帯数累計比、縦軸に所得額の累計比を取り、世帯間の所得分布をグラフ化したものです。

社会に所得格差がなく、所得の分布が完全に平等であれば曲線は対角線（均等分布線）に一致します。

所得の分布に偏りがある場合下方に凸のグラフが現れます。

格差が大きいほど下に大きく膨らんだ形になります。

下の図の紫の補助線に注目すると、この図では全体の中で所得の少ない60％の人たちの所得合計は全体の20％程度しかないことが分かります。

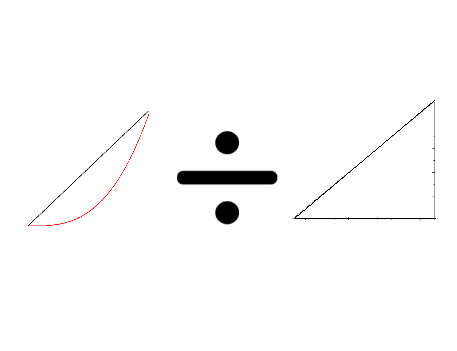
ジニ係数は、均等分布線とローレンツ曲線に囲まれた面積を均等分布線の下の三角形の面積で割ったもので、0～1の値を取ります。

所得の格差が小さいほど0に近い値になり、格差が大きいほど1に近い値になります。分かりやすく説明すると下の図のようになります。

現在の日本のジニ係数は約3.4程度であり、世界で上から約15番目となっています。

つまり、ジニ係数のみで所得格差を評価すると15番目に格差が大きい国ということになります。

では、実際にジニ係数を算出してみましょう。横軸を$x$、縦軸を$y$と定義します。

ここでは分かりやすく赤線で示されるローレンツ曲線を$y＝x^{3}$と近似できるとして計算します。

ｘ範囲を０→１として定積分を行うと

$$S１＝\int_0^1 x dx－\int_0^1 x^{3} dx＝\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$$

三角形の面積は底辺×高さ÷２なので

$$S2＝1\times1\div2=\frac{1}{2}$$

求めるジニ係数は

$$S1\div S2＝\frac{1}{4}\div\frac{1}{2}＝\frac{1}{2}＝0.5$$

となります。

経済学で所得格差を表すローレンツ曲線とジニ係数についてお話してきました。

格差が大きいと貧困や争いの原因となりますが、多少の格差は労働意欲の向上にもつながるため、必ずしも平等であることが正しいというわけではありません。

適切な格差を見極め、所得税や消費税などの分配制度を適用することで上手にコントロールしていくことが大切なのではないかと思います。